《高等数学A1》课程思政案例——洪光焱
“课程思政”案例设计
案例名称:复合函数的导数
主讲教师:洪光焱
课程名称:高等数学A1
课程性质:公共基础课
适用专业:工科各本科专业
所属类别:理学
一、课程简介
《高等数学A1》是工科类各本科专业的通识必修课,具有较强的理论性、抽象性和应用性,是培养高层次科技人才数学素养的基础课程。该课程介绍一元函数微积分及其应用的基础知识,训练学生的基本运算技能和思维能力。主要内容包括函数与极限、导数与微分、微分中值定理与导数的应用、不定积分、定积分、定积分的应用、微分方程等。
二、思政元素挖掘与思政素材选取
适时介绍相关的数学史知识,激励学生学习科学家勇于探索、追求卓越的创新精神,培养实事求是、谦逊严谨的治学态度。综合运用各种教学方法,引导学生体会和欣赏数学中的形式美、理性美,激发学习热情,陶冶审美情操。关注数学基本概念之间的联系,帮助学生进一步树立辩证唯物主义的价值观念。
三、课程思政案例设计与实施
1.案例教学目标
掌握复合函数求导数的链式法则,培养严谨细致的治学态度。
2.教学方法
以讲授法为主,在定理推导和例题演示之后组织课堂练习,使用多媒体课件展示相关素材。
3.教学过程
首先,复习回顾函数算术运算的求导法则和反函数的求导法则。可以采用提问的方式,引导学生一起回顾。接着,引入复合函数求导的链式法则,讲解该法则的推导证明。再而,列举两个例题,演示链式法则的使用方法。最后,组织课堂练习,训练学生运用链式法则的技巧,巩固学习效果。
定理:设函数在点处有导数,函数在点处有导数,则复合函数在点处有导数,且
证明:设自变量在点处有增量,相应的函数和分别有增量:
其中.因为函数在点处有导数,从而它在该点处连续,所以当时.以下分两种情况讨论:
根据极限的保号性质,当足够小时,保持一定的正负符号,此时.应用复合函数的极限定理,有
于是
由于,根据极限的有界性质,当足够小时,
其中为某个常数.因此,当足够小而异于时,有
上述不等式对明显也是成立的,也就是说上述不等式对足够小的都成立.注意到,当时,这意味着只要足够小,就能满足前面的要求.于是,当足够小时,
当时,上式右端是趋于的,从而左端也趋于.因此
前述两种情形,都证明了是复合函数在点处的导数.
例题1:求函数的导数.
例题2:设函数有导数,且,则(对数导数)
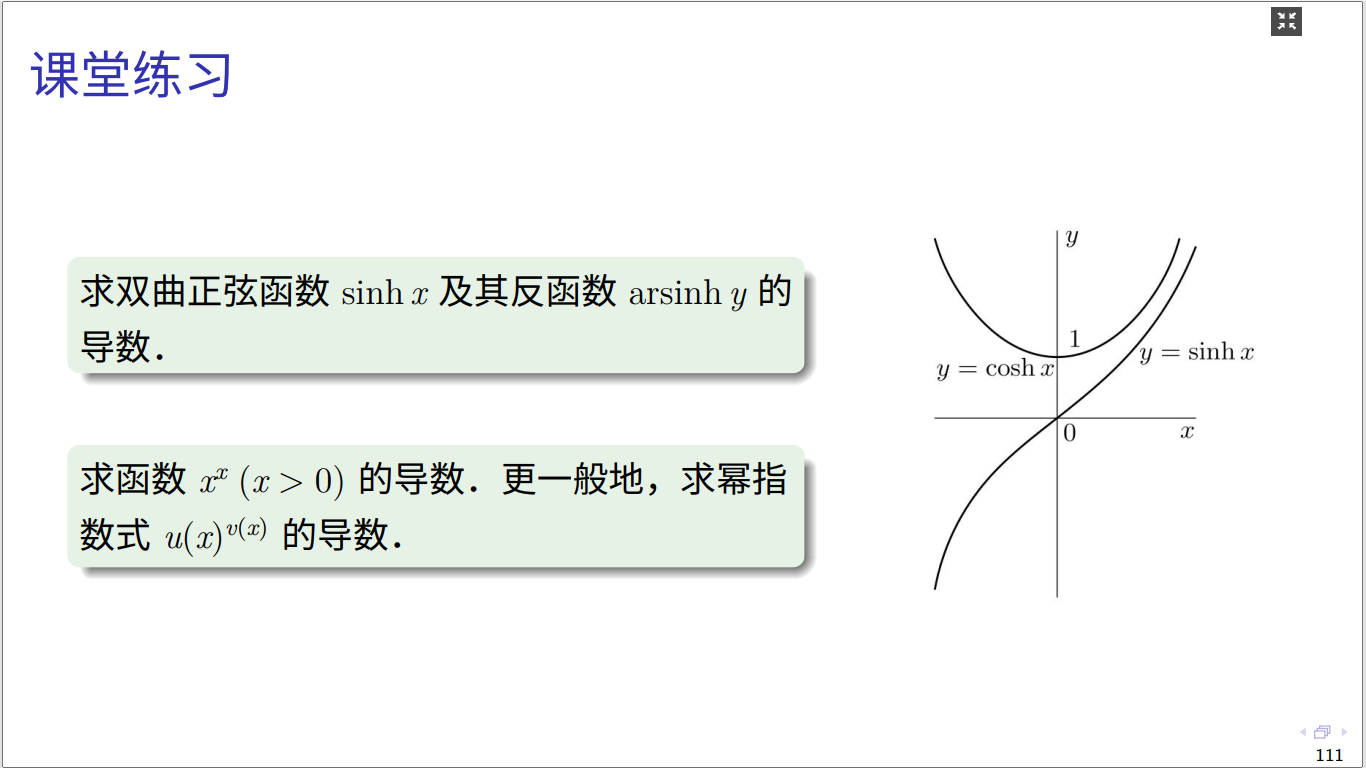
练习1:求双曲正弦函数及其反函数的导数.
练习2:求函数的导数.更一般地,求幂指数式的导数.
4.课程思政内容及融入方式
在讲解导数链式法则的严格推导证明之后,对比某些教材给出的不完整证明,提醒学生注意其中复合函数极限定理的应用细节,训练学生的逻辑推理能力,培养学生严谨的科学精神。
5.教学效果分析及教学反思
本案例呈现复合函数求导法则的教学,在讲解数学定理的严格推导过程中,自然地融入严谨细致的治学态度的培养引导。经过教学实践,学生能比较完整地掌握相应的知识点,基本达到预期的教学目标。
图1 理论讲解
|
图2 例题演示
|
图3 课堂练习
|